Sacred Geometry , music and a possible correlation with
quantum-mechanics
Version 1.2 , July 1997 by Martin Euser.
In this article I will introduce a simple formula of Sacred Geometry which has
interesting properties. I will not provide an extensive introduction to the
concept of Sacred Geometry since there are many websites where you can find
introductory material into this field.
Instead of that I will, however, provide some links to interesting material
(new developments in this area of research).
The basic idea of Sacred Geometry is summed up by Plato:
'The Demiurgos geometrizes'.
Now, the Demiurgos, often erroneously translated as "God", is simply
the collective
host of beings that is sometimes referred to as 'the Architects' or the third
(manifest) logos of our cosmos.
In the Biblical Genesis we find the term 'Elohim', which again is erroneously
translated as "God". Instead, it can be better translated as 'host
of angelic beings' which formed mankind in their image.
This, of course, is a story in itself and more details can be found in Ralston
Skinner's work 'Source of Measures', Gottfried de Purucker's 'Fundamentals of
the esoteric philosophy', Alvin Boyd Kuhn's writings, Gerald Massey's writings
and Helena Petrovna Blavatsky's writings such as 'Isis Unveiled' and
"Secret Doctrine'(the last book being rather mystical in nature and
generally being little understood). See my other articles for links to
websites with writings from some of these authors.
Now, the question is, 'How does the demiurgos geometrize?'
What are the ways and methods which are used in or through the Minds of the
intelligences that have prepared the design for our earth, man, flowers,
animals, minerals, etc.?
This question has occupied many minds , from the old Hindus to the
Babylonians, Greeks, Jews, to the modern student of Sacred Geometry. Some
(partial) answers seem to have been found and laid down in architectural
designs to be found in Hindu temples, Egyptian pyramids, etc., and coded into
scriptures as the Bible, the Hindu Puranas, etc.
See e.g. the above mentioned work of Skinner. For the keen observer it is very
clear that there is an inherent order in this universe although there
may appear to be chaotic phases due to the interactions of a multitude of
factors, wills, energies, etc.
The growth and development of a human embryo is a good example of the
harmonious workings of nature. In the beginning stage, the cells are
configured in a beautiful geometrical pattern, reminding one of the structures
that are found in the mineral kingdom. Later on in the developmental stage one
can observe structures reminding one of plants, lower animals, etc.
culminating in the fully developed foetus. Michael Schneider has written a
beautiful book on Sacred Geometry which illustrates features such as the
above.
He wrote "A Beginner''s Guide To Constructing The Universe" (HarperPerennial)
Some websites relating to the book & Michael:
www article:
Cosmic
Dozens: Twelve-Fold Designs of Society and Art
Workshop:
Sacred Harmony: The Patterns
of Nature and the Ways of Knowing
Book Reviews:
A Beginner's Guide to Constructing the Universe: The Mathematical
Archetypes of Nature, Art, and Science (A Voyage From1 To 10)
Book review by David Fideler,
reprinted from PARABOLA (Winter 1995)
Michael's workshops
in northern CA
Another classic on Sacred Geometry is Doczi's book 'The power of limits'
which richly illustrates the harmonies in nature, art and architecture.
Manifestation means limitation and thus the title of the book was enough
incentive for me to buy it and have a look at it. Doczi develops the idea of dinergy
and patterns of sharing. Dinergy refers to the working of opposites united in
a harmonious proportion. An example is the working of the minor and major
parts of the golden proportion. He invented the word 'dinergy' to refer to the
universal pattern-creating process.
As a prefatory remark to what follows I want to add that I don't believe
that one magical mathematical formula exists which explains all and
everything. The Boundless has an infinite number of attributes and its
emanations vary accordingly. Yet we are told that analogy seems to be the
guiding principle in the emanation and building of worlds, forms, etc.
Infinite variation along analogical lines (nature repeats itself in endless
variations) may be the answer to the question of the operations in/of the
Divine Mind and more specifically pertaining to the operations of the Builders
, but more research is necessary. The emergence of fractal theory seems to be
an interesting development in this respect. Fractals embody the principle of
repetition so abundantly present in nature.
The theosopher Gordon Plummer has shown that the dodecahedron is capable of
generating the icosahedron, and these two Platonic solids together, the other
Platonic solids (tetrahedron, cube, octahedron) through the working of the
well-known number Phi (the golden section number).
The dodecahedron and icosahedron can generate each other in an infinite series
through a repeated geometrical process where the Phi proportion plays a
dominant role.
His "Mathematics of the Cosmic Mind' is interesting food for thought.
Some independent researchers have followed up on his ideas and also try to
combine ideas from Sacred Geometry with chaos theory and fractals. An
interesting example of this can be found at : San
Graal School for Sacred Geometry
Another example of Sacred Geometry , applied to the Platonic solids and the
Kabbalistic Tree of Life , can be found at: Sacred
Geometry discovery
Now I come to my own , thus far limited research in the area of Sacred
Geometry.
While studying the Secret Doctrine of Blavatsky, I discovered her mentioning
something about seven being the root number of formation. Being engaged in a
little study of Greek geometrical concepts, like arithmetic mean, geometrical
mean and harmonic mean, I decided to do a little research on the root of seven
( 7 ) and this proved to be the start of some interesting discoveries.
Figure 1 shows the relation of these means to each other: 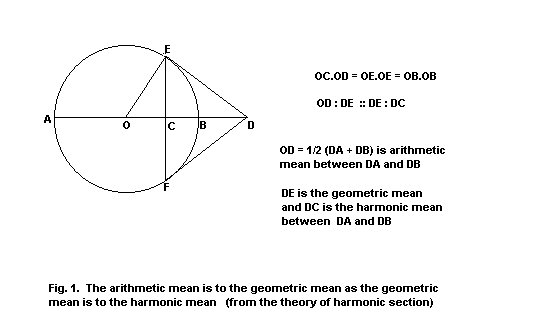
I will sketch some highlights of my findings, which form only the proverbial
tip of the iceberg.
The next section presupposes a basic interest in and acquaintance with high
school mathematics. I'll skip the derivations of the results (which are very
easy to obtain, however).
First of all, I started with the idea that Pythagoras' famous musical
proportions might be found by using the idea of arithmatical, geometrical and
harmonic means generated from a pair of numbers (two poles or a pair of
lines) , thus:
A - n .V(7) and A + n .V(7) <P> where A is the arithmetical mean of this
pair and V is the symbol for taking the square root (in this
case of the number seven).
I found out that the following two poles had a relation to the major third
(which is a proportion of 4:3) :
16 - 4.V(7) and 16 + 4.V(7) ( the '.' is a symbol for multiplication)
This pair of numbers yields the following means:
A = 16 ; G = 4 * 3 = 12 ( '*' is symbol for multiplication) and H = 9
G means the geometrical mean for the two poles and H indicates the harmonic
mean.
The formulas for G and H are in this case:
G = V( 16² - 16 * 7) and H = G²/ A
Now, 16:12 is 4:3 and 12:9 is 4:3 , so the 4:3 proportion is implied.
This result encouraged me to research further pairs of numbers and I found
some interesting poles with properties as follows:
9 - 3. V(5) and 9 + 3.V(5) have A= 9, G= 6 and H= 4 which imply
a relation of 9:6 = 3:2 and 6:4 which again is 3:2. This is the proportion for
the quint or fifth in music!
I'll spare you some details of research and present the abstracted general
formula capable of generating musical proportions:
The poles N² - N * V(2N-1) and N² + N * V(2N-1) generate the following
means:
A = N² , G² = N² * (N -1)² , H = (N-1)²
G = N * (N -1)
Note the beautiful interplay of terms here: substitute N + 1 for N and H
becomes N which is the value of A for N proper.
For N=2 we get : A = 4, G = 2, H= 1 which implies 4:2 = 2:1
In other words, the idea of an octave!
N =3 yields the proportion of the fifth as I've shown already, N = 4 yields
the major third proportion in music. N = 5 yields the 5:4 proportion which
Pythagoras seemed to dislike, but was incorporated in the musical scheme of
another Greek School of philosophy as being a natural proportion.
However the case may be, the famous 9:8 proportion (the distance between two
notes on the major scale) is generated when N=9.
So far for music. As an aside: the root-scheme includes all the roots of
uneven numbers including the famous ones in Sacred Geometry. The only root
missing is 2 which is symbolical for a square. I suspect that there is another
principle to be synthesized into my little theory - some formula containing
this root-number and maybe some squaring function. Systems interacting, so to
speak. (a small part of this has been solved by me now, but that's material
for a second article on Sacred Geometry).
I did some more research on this generative set of poles and discovered some
more interesting properties. When researching the presence of cyclicity in the
generated means by use of this type of scheme (I call it the 'root-number
scheme ') I discovered that it seemed to have a relation to the famous
periodic shell-number in quantum-mechanics:
2 * N²
First electronic shell for N =1 has 2 'positions' for electrons (1S- shell)
Second electronic shell for N=2 has 8 'positions' for electrons (2S-shell
allows two orientations of spin) and 1P shell (allows 3* 2 or six
orientations)
And so on.
What I discovered was that by varying on the above mentioned scheme by
introducing a factor m a new feature arose:
N² - m.N * V(2N-1) and N² + m. N * V(2N-1)
where m is an integral number .
Now, G and H depend on m besides N as to their value. I discovered that by
setting m = N (which is the maximum value of m that is possible without
making G negative) and substituting 2.N² for N yields integral values of G
and H :
(2*N²)² +- N.2.N² * V(4N²-1)
which renders:
A= (2N²)² ; G = (2N²)*N ; H = N²
which again shows an interesting relation between A and H: H has now the same
numerical value as A has in the previous scheme. Somehow there seems to be an
interplay between the schemes in such a way that the arithmetic mean and the
harmonious mean take each other's value.
This makes sense to me, however, as I think that everything in nature is
connected to each other and the above mentioned interplay would fit perfectly
into nature's wondrous works. BTW, if you care to research the values for A, G
and H in this case you will find musical harmonies again!
I have not as yet deeply investigated the relation between the above scheme
and quantum-mechanics (QM) except for noting the interesting results for H
being equal to N² for certain values of N , namely where A=(2N²)², and
discovering the limited allowed values for m: m >= -N and m <= N which
reminds me somewhat of the number of allowed values for the projection of
orbital angular momentum of a particle, say an electron, on the z-axis of a
Cartesian coordinate-system (although we need a third variable to establish
this connection - the angular momentum quantum number l). This is speculative,
of course, but not as weird as it may seem to be. Motion might be described by
a new kind of formalism which connects natural phenomena in a clearer way than
has been established up to now, i.e. underlying forces, patterns, etc. may be
supposed to exist in order to describe the connections between the rich
variety of phenomena that we observe (and who says that we are aware of all
these phenomena?)
Now, N² is a term which appears in the equation for the energy states of a
hydrogen atom :
EN = constant/ N²
Spectral emission occur when an electron falls from a higher energetic level
to a lower one. The frequency of the spectral line (for hydrogen) is simply
given by:
frequency = C ((1/ N)² - (1/ M)²) where N and M are integral numbers > 0
and M > N.
Actually, I suspect that relations such as I discovered may be connected to
orbital motion, be it of electrons or of planets and possibly with rotations
around the own axis of these bodies (which are called 'spin' in the case of
subatomic particles such as electrons).
Time and inspiration permitting I may do some more research in this area.
I need to mention another relation between G² and A:
(G² )² / A ³ = ¼ which is interesting since it reminds me of the famous
law of Keppler: the quotient of squared time of revolution and long semi-axis
of orbit of the planets around the sun to the third power is constant. He
derived the elliptic motion of the planets from this empirical fact and some
other ones. Don't bother about the number ¼: the original form of the
root-scheme can be multiplied by a constant without any essential change as to
the results. Admittedly speculative, but a whole field of research opens to
the open-minded researcher. After all, titanic intellects such as those of
Pythagoras spoke of the music of the spheres and this is just what the
root-scheme formulas seem to be about: harmonic proportions in nature.
The same proportion for G and A can be derived for subsystems of the
root-scheme.
I leave this as an exercise to the mathematically inclined readers.
Schemes as the above are known (in a general sense) in the algebraic theory of
groups. I've not yet researched all the mathematical properties (as to group
properties, subgroups, cyclicity, existence of unity element, etc.) of this
type of system. The system will probably have to be extended with other
factors, elements of interaction, etc.
To the student of Sacred Geometry: there seems to be a beautiful element of
squaring involved here. Finding a root is related to squaring, since the
squaring of a root yields the original number from which the root has been
extracted. Squaring and taking the square root of numbers are inverse
functions, which very much seem to have a place in sacred-geometry. The play
of nature (according to the pattern in the mind of the Demiurgos), I suppose.
This squaring and finding a root must be brought into relation with circles
and spheres, or circular/ spherical motion to make it produce natural
phenomena such as harmonic motion, spirals, etc. This should be the subject of
deep investigation, I think, the more so since scientists have got stuck in
their paradigms and may need to get an impulse from alternative researchers to
establish new paradigms pertaining to nature.
I almost forgot to mention that the ancient Greeks seemed to attach much value
to surface and perimeter of geometrical figures. I have related these two with
the harmonic mean as follows (for square and rectangle, but the same deduction
can be made for circle and ellipse):
Let a be the side of a square, b and c the sides of a rectangle.
Demand the invariance of proportion between surfaces and surfaces and
perimeter to perimeter of square and rectangle.
Then it follows that: 4a / (2b + 2c) = a²/ (bc)
Elaborating this gives: 2bc/(b+c) = a which is equivalent to:
a = bc/((b+c)/2) which is the formula for the geometrical mean for the
poles:
½(b+c) +/- ½(b-c)
So, ½(b+c) is the arithmetical mean here, being the ¼ part of the perimeter
of a rectangle, so to speak an average of the four sides..<P>
